AdvancedMathModifiedBesselI Method

public static double ModifiedBesselI(
	double nu,
	double x
)

Public Shared Function ModifiedBesselI ( 
	nu As Double,
	x As Double
) As Double

public:
static double ModifiedBesselI(
	double nu, 
	double x
)

static member ModifiedBesselI : 
        nu : float * 
        x : float -> float 

Parameters

nu  Double

The order parameter.

x  Double

The argument, which must be non-negative.

Return Value

The modified Bessel functions appear as the solutions of hyperbolic differential equations with cylindrical or circular symmetry, for example the conduction of heat through a cylindrical pipe.

The regular modified Bessel functions are related to the Bessel functions with pure imaginary arguments.

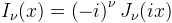
The regular modified Bessel functions increase monotonically and exponentially from the origin.

Because they increase exponentially, this function overflows for even moderately large arguments. In this regeime, you can still obtain the value of the scaled modified e^-x I_ν(x) by calling ScaledModifiedBesselI(Double, Double).

Reference

Other Resources