AdvancedMathHypergeometric2F1 Method

public static double Hypergeometric2F1(
	double a,
	double b,
	double c,
	double x
)

Public Shared Function Hypergeometric2F1 ( 
	a As Double,
	b As Double,
	c As Double,
	x As Double
) As Double

public:
static double Hypergeometric2F1(
	double a, 
	double b, 
	double c, 
	double x
)

static member Hypergeometric2F1 : 
        a : float * 
        b : float * 
        c : float * 
        x : float -> float 

Parameters

a

Type: SystemDouble
The first upper parameter.

b

Type: SystemDouble
The second upper parameter.

c

Type: SystemDouble
The lower parameter.

x

Type: SystemDouble
The argument, which must be less than or equal to one.

Return Value

The Gauss Hypergeometric function is defined by the hypergeometric series:

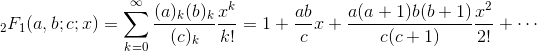
For generic values of a, b, and c, the Gauss hypergeometric function becomes complex for x > 1. However, there are specific cases, most commonly for negative integer values of a and b, for which the function remains real in this range.

For some arguments, the value of the function depends on the order in which the arguments are regarded as approaching their values. For example, in general, if x = 0, F = 1. On the other hand, in general, if c = -1, F is infinite. If x = 0 and c = -1, the value depends on which limit is taken first.

Our implementation does not achieve full precision in all parameter regions. For |x| < 1/2 and |a|, |b| < 10, we achieve approximately full precision. For |x| > 1/2, we loose about one decimal digit of precision, and for every order of magnitude that |a| or |b| exceeds 10, we loose about one decimal digit of precision.

Reference

Other Resources