Function
Definition
Assembly: Meta.Numerics (in Meta.Numerics.dll) Version: 4.2.0+6d77d64445f7d5d91b12e331399c4362ecb25333
public static OdeResult IntegrateOde(
Func<double, double, double> rhs,
double x0,
double y0,
double x1,
OdeSettings settings
)Public Shared Function IntegrateOde (
rhs As Func(Of Double, Double, Double),
x0 As Double,
y0 As Double,
x1 As Double,
settings As OdeSettings
) As OdeResultpublic:
static OdeResult^ IntegrateOde(
Func<double, double, double>^ rhs,
double x0,
double y0,
double x1,
OdeSettings^ settings
)static member IntegrateOde :
rhs : Func<float, float, float> *
x0 : float *
y0 : float *
x1 : float *
settings : OdeSettings -> OdeResult Parameters
- rhs FuncDouble, Double, Double
- The right hand side function, which returns the value of the derivative given the values of the independent variable and the function.
- x0 Double
- The initial value of the independent variable.
- y0 Double
- The initial value of the function.
- x1 Double
- The final value of the independent variable.
- settings OdeSettings
- The settings to use when solving the problem.
Return Value
OdeResultThe solution, including the final value of the function and its derivative.
Remarks
An ordinary differential equation (ODE) has the form:
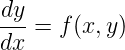
The function specifying the derivative as a function of x and y is called the right-hand-side (RHS).
The integration of an ODE consists of specifying the value of y at some initial x and computing its value at a different x in accordance with the differential equation. The terms "initial" and "final" are derived from the common case where the independent variable is time, but the algorithm works whether the independent variable resents a time, a location, or a completely non-physical quantity, as long as the problem has the form of an ODE.
ODEs involving multiple, coupled dependent variables can be integrated using the IntegrateOde(FuncDouble, IReadOnlyListDouble, IReadOnlyListDouble, Double, IReadOnlyListDouble, Double, MultiOdeSettings) method. Higher order ODEs can be integrated by representing them as coupled ODEs in which the zeroth component is the desired y, the first component is y', the second component is y'', etc. So-called conservative second order ODEs should be integrated using the IntegrateConservativeOde(FuncDouble, Double, Double, Double, Double, Double, Double, OdeSettings) method. If your ODE's RHS depends only on x, the problem reduces to a simple integral, which can be solved more rapidly and accurately using the Integrate(FuncDouble, Double, Interval, IntegrationSettings) method. Analytic techniques can also be used to reduce several other kinds of ODEs to simple integrals or lower-order ODEs.
Exceptions
| ArgumentNullException | The rhs or settings is null. |
| NonconvergenceException | The ODE could not be integrated to the required precision before exhausting the maximum allowed number of rhs evaluations. |