Meta.Numerics Library
Function
Solves a conservative second order ordinary differential equation initial value problem using the given settings.
Definition
Namespace: Meta.Numerics.Analysis
Assembly: Meta.Numerics (in Meta.Numerics.dll) Version: 4.2.0+6d77d64445f7d5d91b12e331399c4362ecb25333
The solution, including the final value of the function and its derivative.
Assembly: Meta.Numerics (in Meta.Numerics.dll) Version: 4.2.0+6d77d64445f7d5d91b12e331399c4362ecb25333
C#
public static OdeResult IntegrateConservativeOde(
Func<double, double, double> rhs,
double x0,
double y0,
double yPrime0,
double x1,
OdeSettings settings
)VB
Public Shared Function IntegrateConservativeOde (
rhs As Func(Of Double, Double, Double),
x0 As Double,
y0 As Double,
yPrime0 As Double,
x1 As Double,
settings As OdeSettings
) As OdeResultC++
public:
static OdeResult^ IntegrateConservativeOde(
Func<double, double, double>^ rhs,
double x0,
double y0,
double yPrime0,
double x1,
OdeSettings^ settings
)F#
static member IntegrateConservativeOde :
rhs : Func<float, float, float> *
x0 : float *
y0 : float *
yPrime0 : float *
x1 : float *
settings : OdeSettings -> OdeResult Parameters
- rhs FuncDouble, Double, Double
- The right hand side function.
- x0 Double
- The initial value of the independent variable.
- y0 Double
- The initial value of the function variable.
- yPrime0 Double
- The initial value of the function derivative.
- x1 Double
- The final value of the independent variable.
- settings OdeSettings
- The settings to use when solving the problem.
Return Value
OdeResultThe solution, including the final value of the function and its derivative.
Remarks
A conservative ODE is an ODE of the form
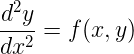
where the right-hand-side depends only on x and y, not on the derivative y'. ODEs of this form are called conservative because they exhibit conserved quantities: combinations of y and y' that maintain the same value as the system evolves. Many forms of Newtonian equations of motion, for example, are conservative ODEs, with conserved quantities such as energy, momentum, and angular momentum. Our specialized conservative ODE integrator is not only more efficient for conservative ODEs, but does a better job of maintaining the conserved quantities.
Exceptions
| ArgumentNullException | The rhs or settings is null. |
| NonconvergenceException | The ODE could not be integrated to the required precision before exhausting the maximum allowed number of rhs evaluations. |