Beta
Definition
Assembly: Meta.Numerics (in Meta.Numerics.dll) Version: 4.2.0+6d77d64445f7d5d91b12e331399c4362ecb25333
public sealed class BetaDistribution : ContinuousDistributionPublic NotInheritable Class BetaDistribution
Inherits ContinuousDistributionpublic ref class BetaDistribution sealed : public ContinuousDistribution[<SealedAttribute>]
type BetaDistribution =
class
inherit ContinuousDistribution
end- Inheritance
- Object UnivariateDistribution ContinuousDistribution BetaDistribution
Remarks
The beta distribution is defined on the interval [0,1]. Depending on its two shape parameters, it can take on a variety of forms on this interval.
The left shape parameter α controls the shape of the distribution near the left endpoint x = 0. The right shapre paramater β controls the shape of the distribution near the right endpoint x = 1. If a shape parameter is less than one, the distribution is singular on that side. If a shape parameter is greater than one, the distribution goes to zero on that side. If a shape parameter is equal to one, the distribution goes to a constant on that side.
If the two shape parameters are equal, the distribution is symmetric.
When both shape parameters are one, the beta distribution reduces to a standard uniform distribution.
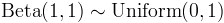
Beta distributions describe the maximum and minimum values obtained from multiple, independent draws from a standard uniform distribution. For n draws, the maximum value is distributed as B(n,1).
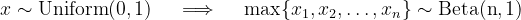
Similarly, the minimum value is distributed as B(1,n).
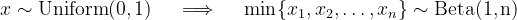
In fact, the ith order statistic (ith smallest value) in n draws from a uniform distribution is distributed as B(i, n - i + 1).
Because of the wide variety of shapes it can take, the beta distribution is sometimes used as an ad hoc model to fit distributions observed on a finite interval.
Constructors
| BetaDistribution | Initializes a new β distribution. |
Properties
| Alpha | Gets the left shape parameter. |
| Beta | Gets the right shape parameter. |
| ExcessKurtosis |
Gets the excess kurtosis of the distribution.
(Inherited from UnivariateDistribution) |
| Mean |
Gets the mean of the distribution.
(Overrides UnivariateDistributionMean) |
| Median |
Gets the median of the distribution.
(Inherited from ContinuousDistribution) |
| Skewness |
Gets the skewness of the distribution.
(Overrides UnivariateDistributionSkewness) |
| StandardDeviation |
Gets the standard deviation of the distribution.
(Inherited from UnivariateDistribution) |
| Support |
Gets the interval over which the distribution is non-vanishing.
(Overrides ContinuousDistributionSupport) |
| Variance |
Gets the variance of the distribution.
(Overrides UnivariateDistributionVariance) |
Methods
| CentralMoment |
Computes a central moment of the distribution.
(Overrides ContinuousDistributionCentralMoment(Int32)) |
| Cumulant |
Computes a cumulant of the distribution.
(Inherited from UnivariateDistribution) |
| Equals | Determines whether the specified object is equal to the current object. (Inherited from Object) |
| ExpectationValue |
Computes the expectation value of the given function.
(Inherited from ContinuousDistribution) |
| FitToSample | Computes the Beta distribution that best fits the given sample. |
| GetHashCode | Serves as the default hash function. (Inherited from Object) |
| GetRandomValue |
Generates a random variate.
(Overrides ContinuousDistributionGetRandomValue(Random)) |
| GetRandomValues |
Generates the given number of random variates.
(Inherited from ContinuousDistribution) |
| GetType | Gets the Type of the current instance. (Inherited from Object) |
| Hazard |
Computes the hazard function.
(Inherited from ContinuousDistribution) |
| InverseLeftProbability |
Returns the point at which the cumulative distribution function attains a given value.
(Overrides ContinuousDistributionInverseLeftProbability(Double)) |
| InverseRightProbability |
Returns the point at which the right probability function attains the given value.
(Overrides ContinuousDistributionInverseRightProbability(Double)) |
| LeftProbability |
Returns the cumulative probability to the left of (below) the given point.
(Overrides ContinuousDistributionLeftProbability(Double)) |
| ProbabilityDensity |
Returns the probability density at the given point.
(Overrides ContinuousDistributionProbabilityDensity(Double)) |
| RawMoment |
Computes a raw moment of the distribution.
(Overrides ContinuousDistributionRawMoment(Int32)) |
| RightProbability |
Returns the cumulative probability to the right of (above) the given point.
(Overrides ContinuousDistributionRightProbability(Double)) |
| ToString | Returns a string that represents the current object. (Inherited from Object) |