OrthogonalPolynomialsChebyshevT Method

public static double ChebyshevT(
	int n,
	double x
)

Public Shared Function ChebyshevT ( 
	n As Integer,
	x As Double
) As Double

public:
static double ChebyshevT(
	int n, 
	double x
)

static member ChebyshevT : 
        n : int * 
        x : float -> float 

Parameters

n  Int32

The order, which must be non-negative.

x  Double

The argument, which must lie in the closed interval between -1 and +1.

Return Value

Chebyshev polynomials of the first kind are orthogonal on the interval [-1,1] with the weight (1-x²)^-1/2.

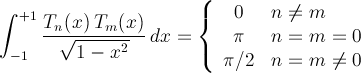
Values returned are fully accurate (14-16 decimal digits) over the full range of argument for orders up to thousands. By orders up to a million, ~11 decimal digits remain accurate.

For high orders, close to the endpoints, the oscillation of Chebyshev polynomials becomes extremely rapid. Particularly in these regions, keep in mind that the nearest representable floating point number might be far enough from the decimal number argument you want that the Chebyshev value shifts significantly. For example, you might claim that our value for T(1000000,0.9999) is accurate only to ~9 digits. But that is because 0.9999 is actually stored as 4503149267407759 X 2^(-52) = 0.99990000000000001101..., and the value returned is indeed accurate for that argument to ~11 digits.

Reference

Other Resources