LUDecomposition Class |
Inheritance HierarchyNamespace: Meta.Numerics.Matrices
Assembly: Meta.Numerics (in Meta.Numerics.dll) Version: 4.1.4
SyntaxThe LUDecomposition type exposes the following members.
Properties
Methods| Name | Description | |
|---|---|---|
 | Determinant |
Computes the determinant of the original matrix.
|
| Equals | Determines whether the specified object is equal to the current object. (Inherited from Object.) |
| GetHashCode | Serves as the default hash function. (Inherited from Object.) |
| GetType | Gets the Type of the current instance. (Inherited from Object.) |
| Inverse |
Computes the the inverse of the original matrix.
|
| LMatrix |
Gets the L factor.
|
| PMatrix |
Gets the permutation matrix.
|
| Solve |
Solves A x = b.
|
| ToString | Returns a string that represents the current object. (Inherited from Object.) |
| UMatrix |
Gets the U factor.
|
RemarksAn LU decomposition is a representation of a matrix M as the product of a lower-left-triangular matrix L and and an upper-right-triangular matrix U. To reduce numerical instabilities, we actually decompose a row-wise permutation of a matrix, so that we have P A = L U, where P is a permutation matrix.
For example, here is an LU decomposition of a permutation of a simple 3 X 3 matrix:
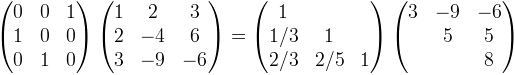
Given an LU decomposition of a permutation A, we can solve systems of linear equations or compute the determinant or inverse of A. LU decomposition is the fastest way to solve an arbitrary system of linear equations. It is much faster, and less subject to rounding errors, to solve Ax=b by LU decomposition than than by inverting A and multiplying A-1b.
You can use the LUDecomposition method to obtain the LU decomposition of any non-singular square matrix.
See Also